5.2 Item parameter estimation

5.2.1 Pairwise estimation of item difficulties

There are many methods for estimating the difficulty parameters of the Rasch estimation. See Linacre (2004) for an overview.

We will use the pairwise estimation method. This method writes the probability that child \(n\) passes item \(i\) but not item \(j\) given that the child passed one of them as \(\exp(\delta_i) / (\exp(\delta_i) + \exp(\delta_j))\). The method optimizes the pseudo-likelihood of all item pairs over the difficulty estimates by a simple iterative procedure.

Zwinderman (1995) has shown that this procedure provides consistent estimates with similar efficiency computationally more-intensive conditional and marginal maximum likelihood methods.

The beauty of the method is that it is independent of the ability distribution, so there is no need to remove perfect scores. We use the function rasch.pairwise.itemcluster() as implemented in the sirt package (Robitzsch 2016).

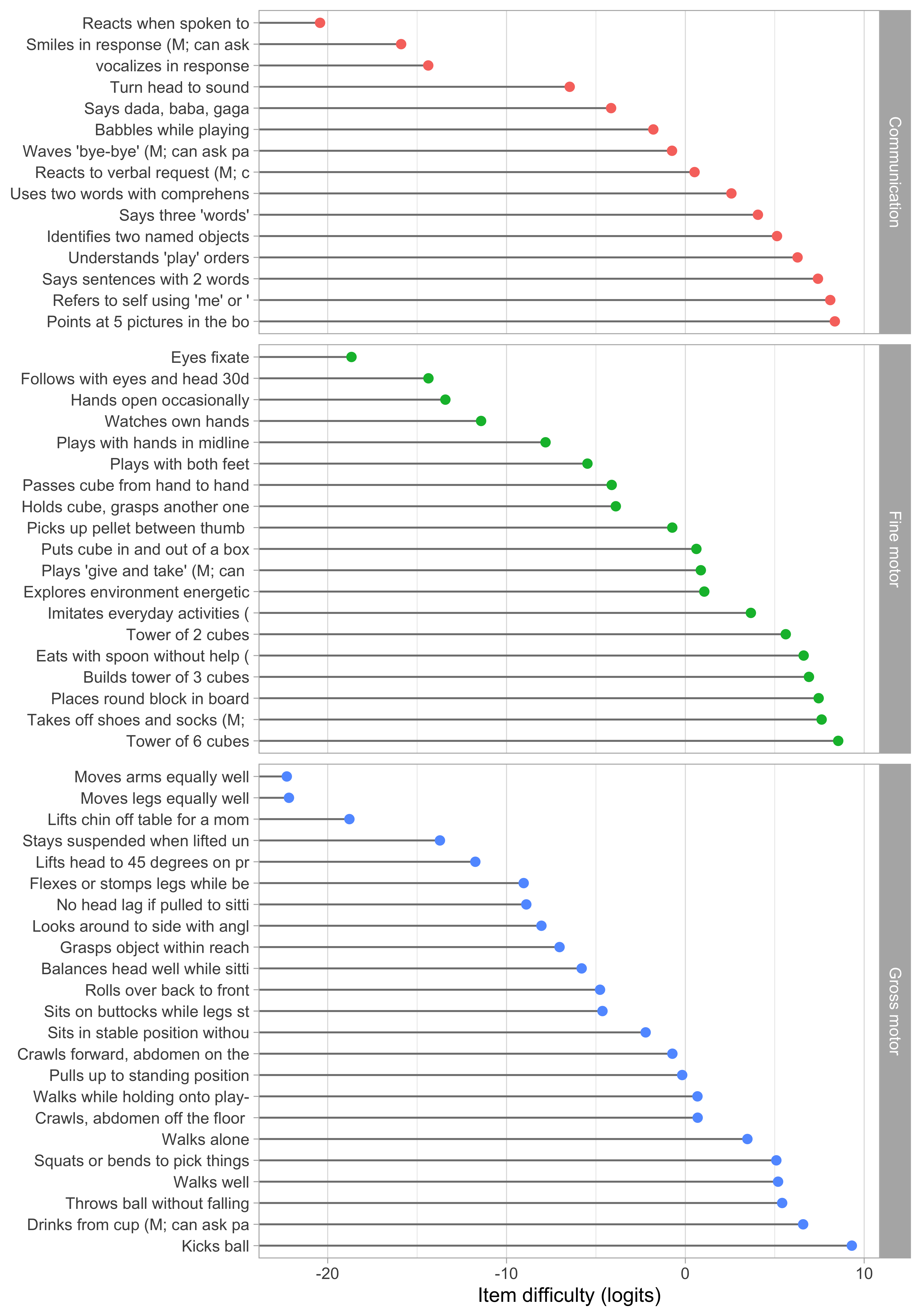
Figure 5.1: Estimated item difficulty parameters (\(d_i\)) for 57 milestones of the DDI (0 - 2 years).

Figure 5.1 summarizes the estimated item difficulty parameters. Although the model makes no distinction between domains, the results have been ordered to ease spotting of the natural progression of the milestones per domain. The figure also suggests that not all domain have equal representation across the scale. For example, there are no communication milestones around the logit of \(-10\).

5.2.2 Anchoring

The Rasch model identifies the item difficulties up to a linear transformation. By default, the software produces estimates in the logit scale (c.f. Figure 5.1). The logit scale is inconvenient for two reasons:

• The logit scale has negative values. Negative values do not have a sensible interpretation in child development, and are likely to introduce errors in practice;
• Both the zero in the logit scale, as well as its variance, depend on the sample used to calibrate the item difficulties.

Rescaling preserves the properties of the Rasch model. To make the scale independent of the specified sample, we transform the scale so that two items will always have the same value on the transformed scale. The choice of the two anchor items is essentially arbitrary, but they should correspond to milestones that are easy to measure with small error. In the sequel, we use the two milestones to anchor the D-score scale:

With the choice of Table 5.2, D-score values are approximately 0\(D\) around birth. At the age of 1 year, the score will around 50\(D\), so during the first year of life, one \(D\) unit corresponds to approximately a one-week interval. Figure 5.2 shows the difficulty estimates in the D-score scale.

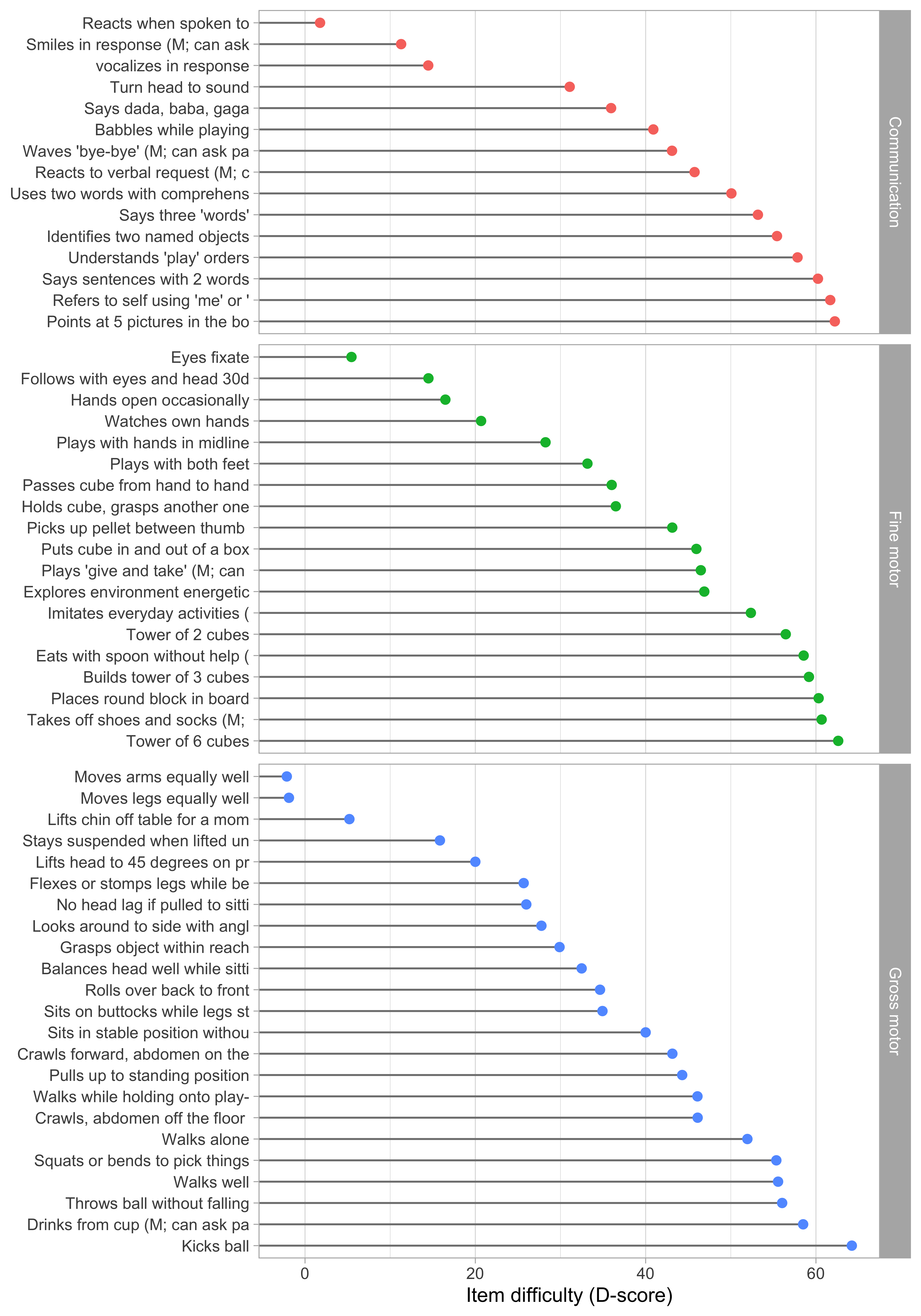
Figure 5.2: Estimated item difficulty parameters (\(d_i\)) for 57 milestones of the DDI (0 - 2 years). Milestones ddigmd057 and ddigmd063 are anchored at values of 20\(D\) and 40\(D\), respectively.