6.2 Person fit
Person fit quantifies the extent to which the responses of a given child conform to the Rasch model expectation. The Rasch model expects that a more able child has a higher probability of passing an item than a less developed child. Person fit analysis evaluates the extent to which this is true.
6.2.1 Person infit and outfit
In parallel to item fit, we can calculate person infit and person outfit. Both statistics evaluate how well the responses of the persons are consistent with the model. Outlying answers that do not fit the expected pattern increase the outfit statistic. The outfit is high, for example, when the child fails easy items but passes difficult ones. The infit is the information weighted fit and is more sensitive to inlaying, on-target, unexpected responses.
Similar to item fit, person fit is also calculated from the residuals, but aggregated differently. We calculate person infit as
\[\mathrm{Person\ infit} = \frac{\sum_{i}^L (x_{ni}-P_{ni})^2}{\sum_i^L W_{ni}}\]
and person outfit as
\[\mathrm{Person\ outfit} = \frac{\sum_{i}^L z_{ni}^2}{L}\]
A threshold for person fit > 3.0 is customary to clean out children with implausible response patterns.
6.2.2 Person infit and outfit in the DDI
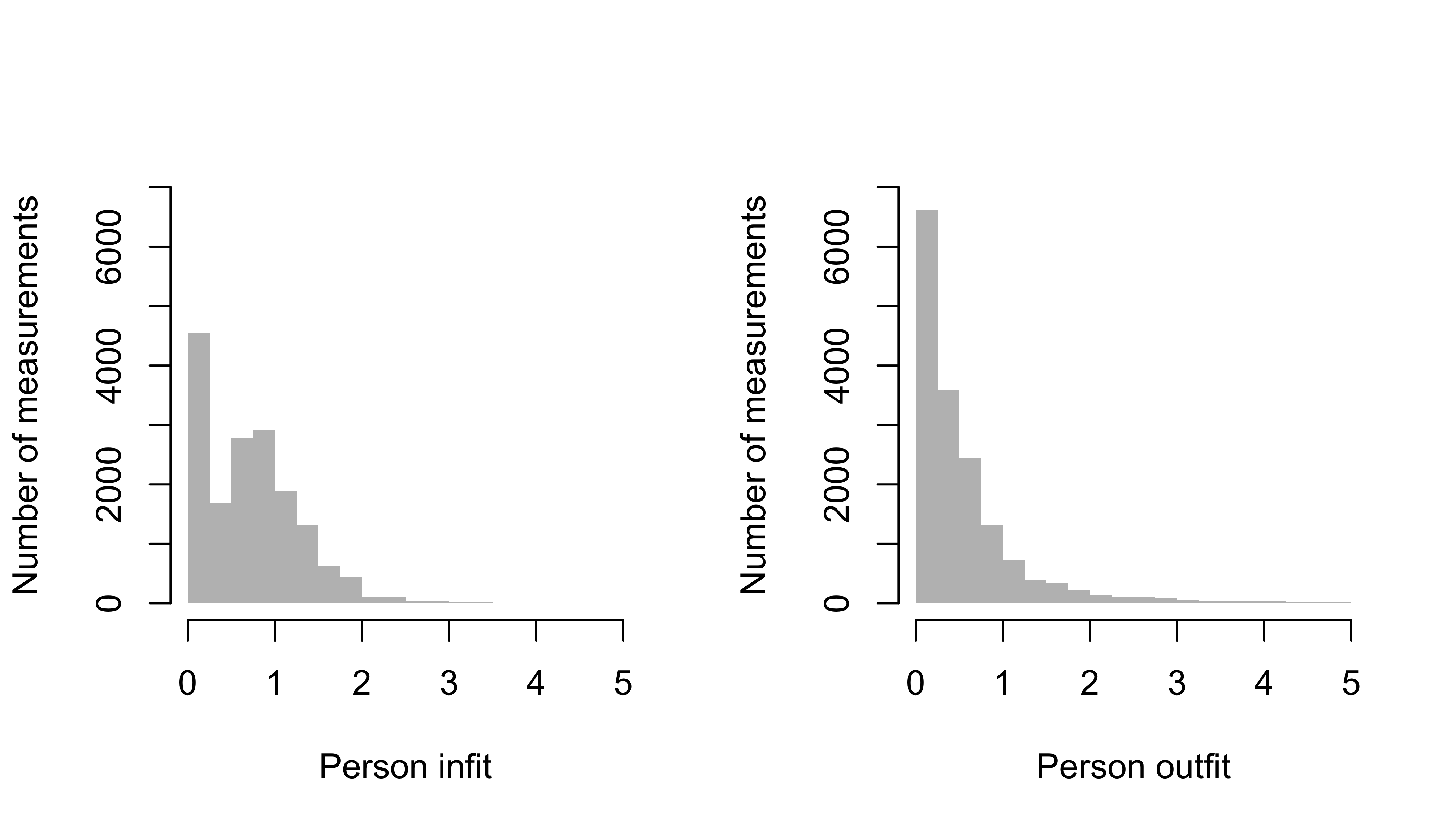
Figure 6.5: Frequency distribution of person infit (left) and person outfit (right) for 16538 measurements of the DDI (SMOCC data).
Figure 6.5 displays the frequency distribution of person infit and person outfit 16538 measurements of the DDI in the SMOCC data. The majority of the values falls below 3.0. For infit, only 43 out of 16538 fit values (0.3 per cent) is above 3.0. There are 446 out of 16538 outfit value (2.7 per cent) above 3.0. Expect the solution to improve after deleting these measurements.