6.4 Item information

6.4.1 Item information at a given ability

Items are generally sensitive to only a part of the ability scale. Item information is a psychometric measure that quantifies how illuminating the item is at different levels of ability. We may visualize item information as a curve per item.

The formula to obtain the item information is the first derivative of the item response curve and can be written as follows:

\[I(\hat\delta_i)=P(\hat\delta_i)(1-P(\hat\delta_i))\],

where \(P(\hat\delta_i)\) is the conditional probability of endorsing item \(i\), and where \(\hat\delta_i\) is the estimated item difficulty in the logit scale. For example for milestone ddicmm039 (“Says three words”) \(\hat\delta_i\) equals \(4.06\).

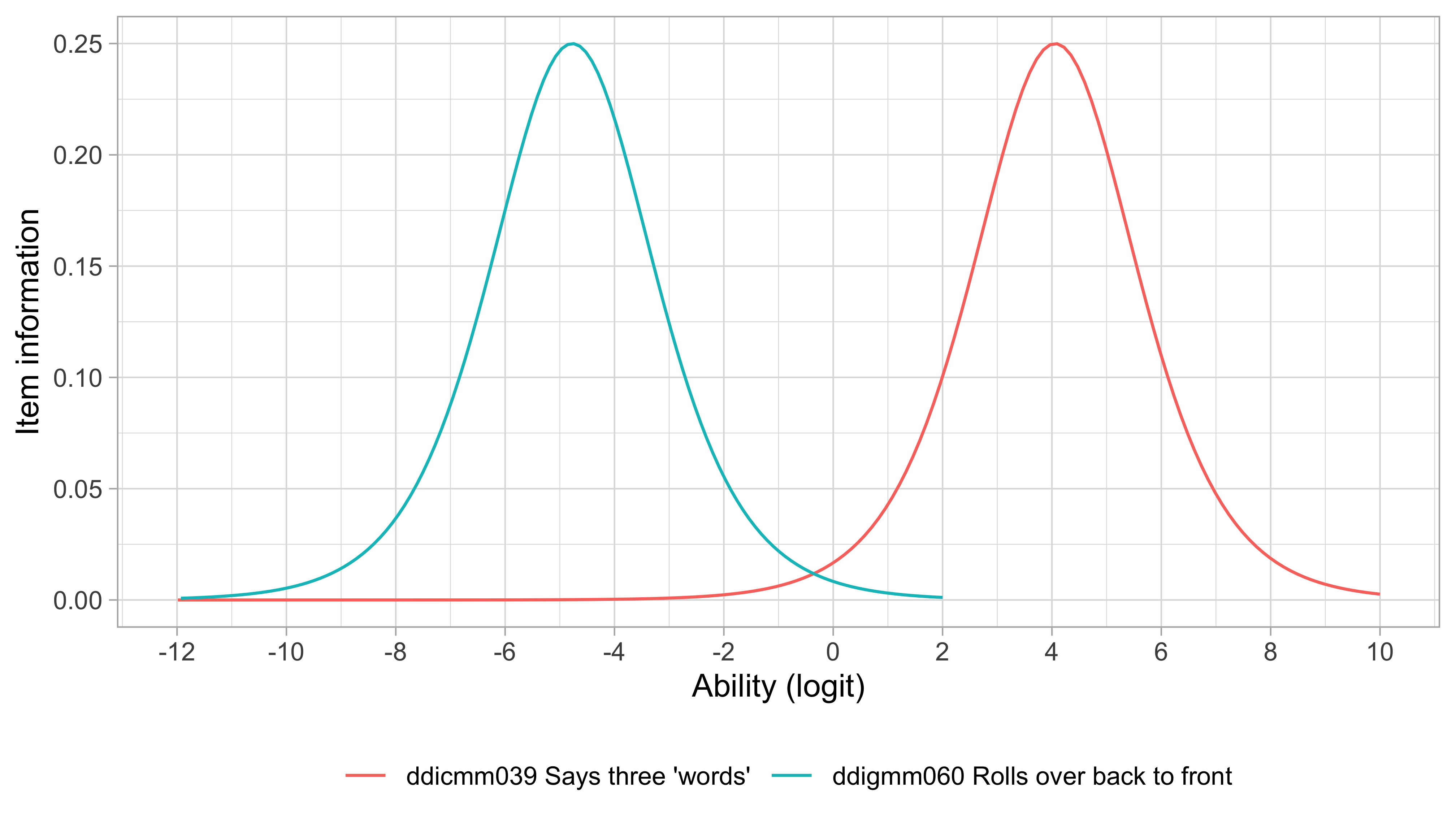
Figure 6.8: The item information curve for two milestones from the DDI.

Figure 6.8 displays the item information curves for two milestones from the DDI. Note that the amount of information for the item is maximal around the item difficulty.

The probability of endorsing milestone ddicmm039 for a child with an ability of \(2\) logits is

\[P_{ni}= \frac{\exp(2 - 4.06)}{1+\exp(2-4.06)} = 0.113\]

At this ability level, milestone ddicmm039 has information

\[I(\hat\delta_i)=0.113 \times (1-0.113) = 0.10\]

6.4.2 Item information at a given age

In practice, it is often interesting to express the item information against age. By doing so, one can identify at what ages an item provides the most information.

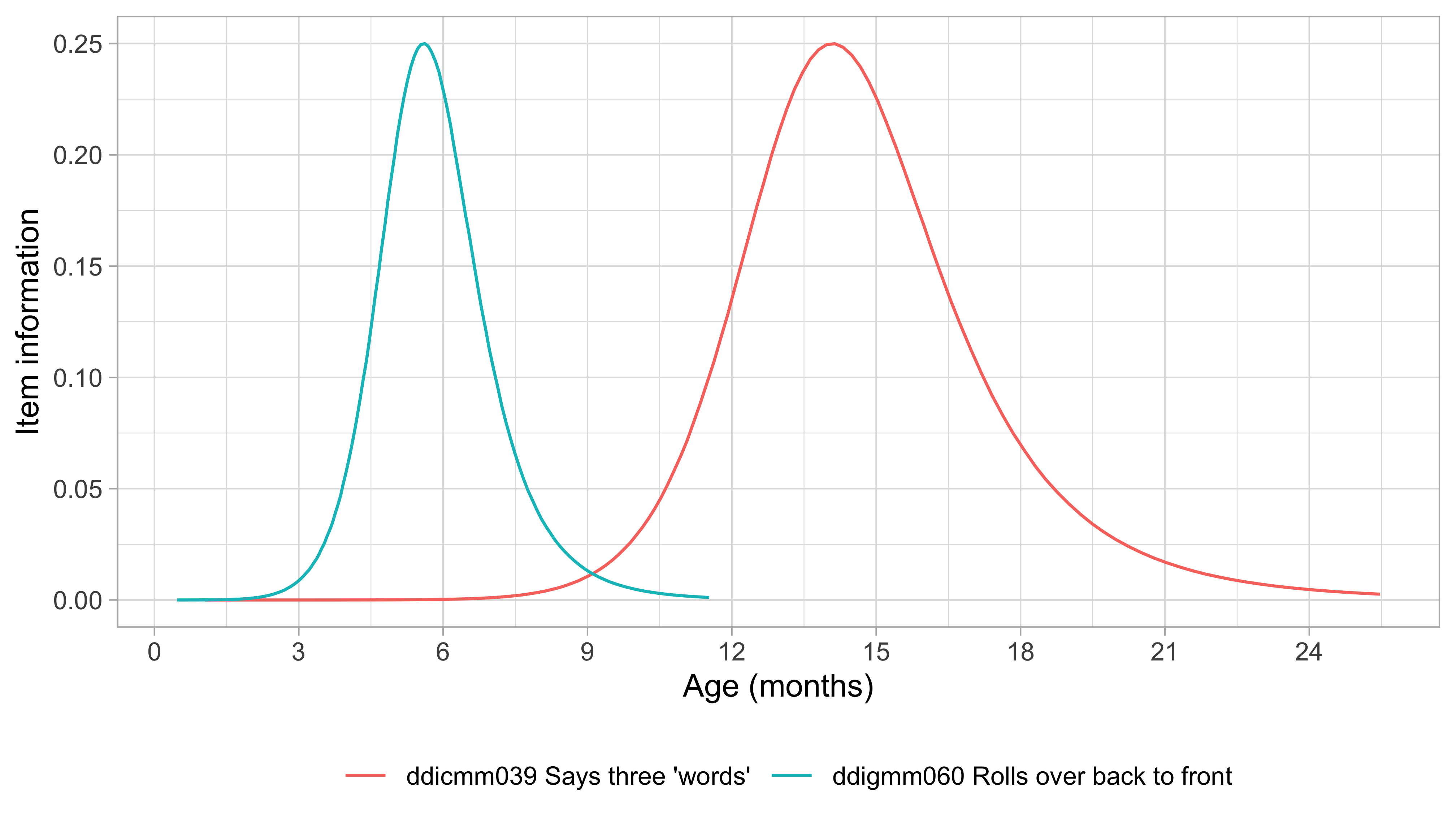
Figure 6.9: Information information of Figure 6.8 plotted against age.

Figure 6.9 shows that the sensitive age ranges differ considerably between items. Suppose we use 0.05 as a criterion. Then ddigmm060 is susceptible between ages 4–8 months, a period of four months. Item ddicmm039 is receptive in the period 10–19 months, a range that is about twice as broad. The symmetric nature of the curves in Figure 6.8 is not present in Figure 6.9. In general, the relation between age and item sensitivity is more complicated than the relationship between ability and item sensitivity.

The item information by age curve helps to determine at what ages we should administer the item. The item will be most informative if delivered at the age at which 50% of the children will pass the milestone. This age corresponds to an item information is equal to 0.5 * 0.5 = 0.25. Administering the item closely around that age provide the most efficient measurement of ability. When space is at a premium (e.g. as in population surveys) using a well-chosen set of age-sensitive milestones will help in reducing the total number of milestones.

In other contexts, milestones may be used as a screening instrument to identify developmental delay. In that case, it is more efficient to administer items that are very easy for the age, e.g. milestones on which, say, 90% of the children will pass.